We will be using pyproj Python library to perform the transformations. This library provides a very handy way of dealing with spatial coordinates transformations. The code example provided is based on pyproj version 2.6.1.
Step 1: Import the necessary libraries.
import pyproj
from IPython.display import HTML
Step 2: Set the input coordinates. You have to replace the easting, northing, and AHD height with your own values.
x = 463802.814 # replace with Easting
y = 6946730.84 # replace with Northing
ahd_height = 80.075 # replace with your AHD height
Step 3: Define the Coordinate Reference Systems (CRS) for GDA2020, MGA2020 Zone 56 and WGS84. We do this by creating objects for each CRS using their Well-Known Text (WKT) representation.
# Create CRS from WKT for GDA2020, MGA2020 Zone 56 and WGS84.
# Here, we're using the WKT definitions provided by the EPSG registry.
gda2020 = pyproj.CRS(
"""GEOGCRS["GDA2020",
DATUM["Geocentric Datum of Australia 2020",
ELLIPSOID["GRS 1980",6378137,298.257222101,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
CS[ellipsoidal,2],
AXIS["geodetic latitude (Lat)",north,
ORDER[1],
ANGLEUNIT["degree",0.0174532925199433]],
AXIS["geodetic longitude (Lon)",east,
ORDER[2],
ANGLEUNIT["degree",0.0174532925199433]],
USAGE[
SCOPE["Geodesy, cadastre, engineering survey, topographic mapping."],
AREA["Australia including Lord Howe Island, Macquarie Island, Ashmore and Cartier Islands, Christmas Island, Cocos (Keeling) Islands, Norfolk Island. All onshore and offshore."],
BBOX[-60.55,93.41,-8.47,173.34]],
ID["EPSG",7844]]"""
)
mga2020_56 = pyproj.CRS("""PROJCRS["GDA2020 / MGA zone 56",
BASEGEOGCRS["GDA2020",
DATUM["Geocentric Datum of Australia 2020",
ELLIPSOID["GRS 1980",6378137,298.257222101,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",7844]],
CONVERSION["Map Grid of Australia zone 56",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",0,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",153,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",0.9996,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",500000,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",10000000,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["(E)",east,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["(N)",north,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Engineering survey, topographic mapping."],
AREA["Australia - onshore and offshore between 150°E and 156°E."],
BBOX[-58.96,150,-13.87,156]],
ID["EPSG",7856]]""")
wgs_84 = pyproj.CRS("""GEOGCRS["WGS 84",
ENSEMBLE["World Geodetic System 1984 ensemble",
MEMBER["World Geodetic System 1984 (Transit)"],
MEMBER["World Geodetic System 1984 (G730)"],
MEMBER["World Geodetic System 1984 (G873)"],
MEMBER["World Geodetic System 1984 (G1150)"],
MEMBER["World Geodetic System 1984 (G1674)"],
MEMBER["World Geodetic System 1984 (G1762)"],
MEMBER["World Geodetic System 1984 (G2139)"],
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]],
ENSEMBLEACCURACY[2.0]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
CS[ellipsoidal,2],
AXIS["geodetic latitude (Lat)",north,
ORDER[1],
ANGLEUNIT["degree",0.0174532925199433]],
AXIS["geodetic longitude (Lon)",east,
ORDER[2],
ANGLEUNIT["degree",0.0174532925199433]],
USAGE[
SCOPE["Horizontal component of 3D system."],
AREA["World."],
BBOX[-90,-180,90,180]],
ID["EPSG",4326]]""")
Step 4: Convert the MGA2020 Zone 56S coordinates to GDA2020 geographic coordinates.
# Create transformer
transformer = pyproj.Transformer.from_crs(mga2020_56, gda2020)
# Transform coordinates to GDA2020 decimal degree
lat, lon = transformer.transform(x, y)
lat = abs(lat)
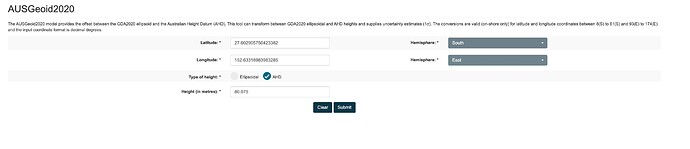
print("Please click on the following link and input the given Longitude and Latitude along with the AHD height to get 'Ellipsoid to AUSGeoid2020 Separation':")
print("\nhttps://geodesyapps.ga.gov.au/ausgeoid2020\n")
print(f"Longitude: {lon}\nLatitude: {lat}\n")
Conversion from GDA2020 MGA Zone 56S to GDA2020
Please click on the following link and input the given Longitude and Latitude along with the AHD height to get “Ellipsoid to AUSGeoid2020 Separation”:
Geodetic Calculators
Longitude: 152.63318983983285
Latitude: 27.602905750423382
This step is crucial because we need the latitude and longitude in the GDA2020 datum, which is required for the next step.
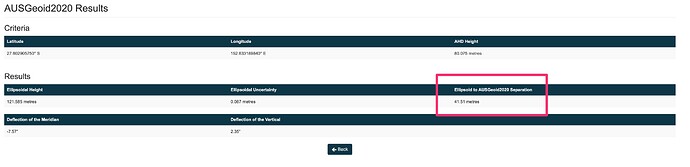
Step 5: Now, we’ll need to obtain the “Ellipsoid to AUSGeoid2020 Separation”. This has to be done manually by entering the latitude and longitude obtained from Step 4 into the AUSGeoid2020 model converter on the Geoscience Australia website (Geodetic Calculators).
Step 6: Convert the GDA2020 geographic coordinates to WGS84, and incorporate the AHD height and the separation obtained from Step 5. ### Enter in the Ellipsoid to AUSGeoid2020 Separation value obtained from the website
# Create transformer
transformer = pyproj.Transformer.from_crs(mga2020_56, wgs_84)
# Transform coordinates to WGS84
lat, lon = transformer.transform(x, y)
geoid_height = 41.51 # replace with the value obtained from the AUSGeoid2020 model
# calculate ellipsoidal height
ellipsoidal_height = ahd_height + geoid_height
print(f"Longitude: {lon}, Latitude: {lat}, Ellipsoidal height: {ellipsoidal_height}")
ANSWER: Longitude: 152.63318983983285, Latitude: -27.602905750423382, Ellipsoidal height: 121.58500000000001
In [12]:
Notes:
- In this step, we use the geoid separation we obtained from the AUSGeoid2020 model. This gives us the difference in height between the AHD (which is close to mean sea level) and the GDA2020 ellipsoid. By adding the separation to the AHD height, we essentially “lift” the point from the AHD to the WGS84 ellipsoid.
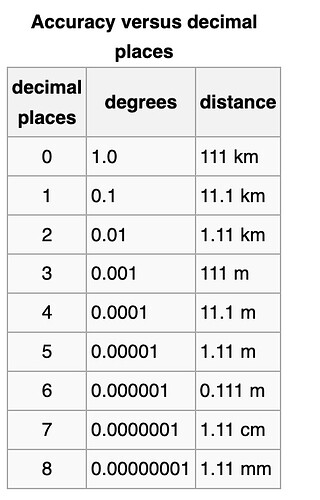
- As for the precision of the coordinates, it can significantly impact the conversion results. The more decimal places we have, the more precise the conversion will be. For instance, if we round off the latitude and longitude to two decimal places, we might end up several kilometers away from the actual location!

I hope this clarifies the process for you! Let me know if you have any further questions!